Arcotangente di -1: Spiegazione semplice con esempi grafici e tattili
Giuseppe Di Grande Aggiornato il 19/06/2025 08:00
L'arcotangente di -1 è -pi/4 (cioè -45°). Perché? Perché la tangente di -pi/4 è -1. L'arcotangente cerca proprio quell'angolo.
- pi è “pi greco” ed equivale a 3,14159265358979. Il pi greco (pi) è una costante matematica che rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro.
- -pi/4 equivale a -0,785398163397448. Rappresenta un angolo espresso in radianti ed è la quarta parte di un angolo giro negativo di pi. Trasformando il valore in gradi otteniamo “-45°”, ossia un angolo di 45° in senso orario (negativo) rispetto all'asse positivo delle ascisse. In trigonometria è spesso usato per indicare angoli nel quarto quadrante del piano cartesiano.
- Arcotangente è la funzione inversa di Tangente. arctan(-1) equivale in radianti a -0,785398163397448 (gradi -45).
- Tangente di -0,785398163397448 equivale a -1. In altre parole, -1 è la tangente di -pi/4.
Cosa significa “arcotangente”
La arcotangente, indicata come arctan, è una funzione matematica che permette di risalire all'angolo a partire dal valore della sua tangente.
La funzione tangente prende un angolo e restituisce un numero: tan(a) = x
La funzione arcotangente fa l'operazione opposta: prende un numero e restituisce l'angolo la cui tangente è quel numero: arctan(x) = a
Quando si applica la funzione tangente a un angolo “a” espresso in radianti, il risultato è un numero reale che rappresenta il rapporto tra il cateto opposto e il cateto adiacente di un triangolo rettangolo con angolo “a”.
Esempi in grafica tattile
Si apra l'ambiente di grafica tattile da Strumenti/Braille/Grafica tattile e si scriva:
a = -pi/4
b = arctan(-1)
MsgBox(a, b)
I due valori a e b sono identici e sono espressi in radianti. Per trasformare un valore radiante in gradi si utilizza la seguente istruzione:
d = RadToDeg(a)
MsgBox(d)
Il risultato è -45
L'inverso di arctan è tan. Per esempio:
c = tan(-pi/4)
MsgBox(c)
Il risultato è -1. Ritrasformabile in -pi/4 con:
b = arctan(-1)
MsgBox(b)
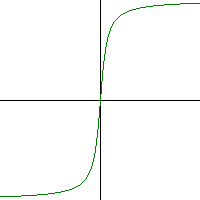
Codice bTactile della curva Arcotangente
#Title: arctan curve y = arctan(x)
#Author: Giuseppe Di Grande
GraphicSize(200,200)
cx = Width / 2
cy = Height / 2
// Draw the centered Cartesian axes
line(0,cy, width,cy)
line(cx,0, cx,height)
// Draw the curve of arctan(x)
ColorPen(clGreen)
x0 = 0
y0 = 0
for x = 0 to width
// Map x from 0-width to -10...+10
vx = (x - cx) / 5
vy = arctan(vx)
// Map vy from -pi/2...+pi/2 to 0...height
sy = cy - ((vy / (pi/2)) * cy)
if x > 0
line(x0, y0, x, sy)
endif
x0 = x
y0 = sy
EndFor
Grafico della curva Arcotangente
Curiosità
L'arcotangente di -1, cioè arctan(-1), è una delle domande più frequenti nei contesti educativi e pratici della trigonometria. Questo valore, pari a -pi/4 (cioè -45°), ricorre spesso perché è un caso semplice, simmetrico e significativo per molte applicazioni.
Viene chiesto spesso perché è un esempio diretto, comprensibile e calcolabile a memoria. L’angolo di -pi/4 è uno dei valori “notevoli” in trigonometria, usato per spiegare concetti come funzioni inverse, quadranti, simmetrie e segni delle funzioni trigonometriche.
In grafica computerizzata, calcolare l’angolo tra due punti richiede spesso la funzione arcotangente. Ad esempio, in videogiochi o interfacce interattive, quando una freccia deve "puntare" verso un obiettivo sullo schermo, si usa spesso la formula arctan(dy/dx), che può restituire proprio -1 in casi simmetrici.
I sistemi di navigazione GPS o le applicazioni di mappatura usano l’arcotangente per calcolare la direzione tra due coordinate geografiche. In zone perfettamente diagonali, l’arcotangente di -1 rappresenta proprio l’angolo di -45° rispetto all’asse positivo.
In ingegneria e fisica, l’arcotangente viene usata nel calcolo della fase nei numeri complessi o nei vettori, ad esempio per determinare la direzione di un campo elettrico, una forza o una velocità.
Anche in grafica vettoriale e nel disegno tecnico, la funzione arctan è fondamentale per determinare inclinazioni e rotazioni. La diagonale con pendenza -1 corrisponde visivamente a una linea inclinata di -45°, molto comune nei layout e nelle composizioni simmetriche.
E per finire, una curiosità tutta speciale: anche nel linguaggio bTactile di Biblos che abbiamo visto, pensato per disegnare grafici tattili che possano essere toccati da persone cieche, l’arcotangente trova il suo spazio! Disegnare un angolo di -pi/4 diventa un modo simpatico per creare una linea inclinata di -45°, perfettamente riconoscibile sotto le dita. Unisce matematica, programmazione e percezione tattile in un’esperienza didattica che… lascia il segno!
Questo articolo è il frutto di conoscenza, esperienza e impegno. Se lo hai trovato interessante, il modo migliore per condividerlo è valorizzarlo: puoi citarne una parte e linkarne la fonte. Solo così offri il giusto riconoscimento a chi lo ha creato.
Per ulteriore supporto ci si può iscrivere nel Gruppo di Biblos su Facebook o nel Canale di Biblos su Telegram.
